Dokumentenverarbeitung

Diese Seite beschreibt unterstützend zu den Terminen die Inhalte des Tutoriums "Computational Intelligence - Document Analysis". Ziel des Tutoriums ist es, gelernte Methoden zu festigen und für ein reales Anwendungsbeispiel, der Dokumentenanalyse, einzusetzen. Dabei werden ebenfalls fachübergreifende Kenntnisse z.B. über Visualisierung in Unity und Java3D vermittelt.

Um den Inhalten folgen zu können, werden Grundkenntnisse in Java oder C# vorausgesetzt.

Das Anwendungsbeispiel

In diesem Tutorium werden die mathematischen Formeln der in den Vorlesungen gelehrten Inhalte in Quellcode umgewandelt und visualisiert. So entwickeln die Studierenden einen anderen Zugang zu den Lehrinhalten. Der Einfluss einzelner Variablen kann dadurch besser erkannt und verstanden werden.
Es wird ein Programm entwickelt, dass Schriftdokumente wie Rechnungen analysiert und entscheidet, ob diese bitonal (zweifarbig), in Graustufen oder farbig gespeichert/gedruckt werden sollen.

Dabei wird es im ersten Schritt in einem Dreidimensionalen RGB-Raum visualisiert. Diesen Farbwürfel voller Pixel kann man durch Mausbewegungen von allen Seiten betrachten. Damit erhält man ein Gefühl für Farbräume und dies dient der besseren Vorstellung und Visualisierung der Cluster, die im nächsten Schritt berechnet werden.

Darstellung eines Bildes im RGB-Farbraum:

Quellen v.l.: Lizenzfreies, bearbeitetes Testbild, Screenshots von eigenem Programm, Screenshot von eigenem Programm

Im zweiten Schritt findet die eigentliche Clusteranalyse statt. Dabei wird das erweiterte Clusterverfahren "Fuzzy K-Means" angewendet. Da es eine Erweiterung ist, wird gleichzeitig ein Verständnis der einfacheren Clusterverfahren vermittelt. Die Datenpunkte werden als Ergebnis in eine bestimmte Menge an Clustern (Gruppierungen) unterteilt. So erhält man Auskunft darüber, wieviele Farben das Bild wirklich definieren. Dies wird im dritten Schritt benötigt.


Quelle: Screenshots von eigenem Programm

Der dritte und letzte Schritt ist es nun, die Informationen der Cluster zu nutzen um die oben genannten Entscheidungen zu treffen. Dabei werden variable Schwellwerte definiert, z.B., dass Dokumente ab einem 15%igen Farbanteil farbig gedruckt werden sollen.

Vorbereitung

Was ist ein Farbraum?

Ein Farbraum ist eine dreidimensionale Repräsentation der Farben. Je nach Farbmodell bietet sich eine andere Form zur Darstellung an. HSV (Hue Saturation Value) lässt sich beispielsweise sehr gut mit einem Zylinder oder Kegel repräsentieren während RGB (Red Green Blue) durch einen Würfel dargestellt wird.

Im Tutorium wird mit dem RGB-Farbmodell gearbeitet. Er ist sehr einfach zu verstehen und zu verwenden. Die Farben werden aus den drei Hauptkomponenten erzeugt:
- R: Rot
- G: Grün
- B: Blau
Eine Erweiterung ist der ARGB-Farbraum, bei dem noch ein A: Alpha-Wert hinzukommt.
Die Werte der jeweiligen Farben liegen zwischen 0 und 255, wobei 0 keine Intensität und 255 volle Intensität der Farbe angibt. Die einfachsten RGB-Farben an denen man sich orientieren kann sind deshalb:
- (255, 255, 255): weiß
- (0, 0, 0): schwarz
- (255, 0, 0): rot
- (0, 255, 0): grün
- (0, 0, 255): blau

Eine Visualisierung im Tutoriumsprogramm: (32*32*32 Werte)

Quelle: Screenshot von eigenem Programm

Entwicklungsumgebungen

Um den Code des Projekts bearbeiten zu können, benötigt man natürlich eine Entwicklungsumgebung. Der Code für die Clusteranalyse und einfache Darstellung wurde für C# und Java entwickelt. Die erweiterte Visualisierung und Verarbeitung wurde mit Unity und C# erstellt.

Die Entwicklungsumgebung für die beiden Programmiersprachen kann man sich nach eigenen Präferenzen auswählen. Empfehlenswert sind dabei NetBeans für Java und Visual Studio für C#. Visual Studio erhält man als Informatik-Student über das Microsoft Imagine Programm kostenlos.

Für die Entwicklung mit Unity ist ein kostenloses Unity-Konto und die Installation des Unity-Editors notwendig.

Clusteranalyse "Fuzzy K-Means"

Theoretische Beschreibung

Die theoretische Beschreibung des Algorithmus findet sich in vielen Quellen online oder in den Folien der Vorlesung.
Nachfolgend ein Link zu Wikipedia, wo die mathematische Beschreibung aufgeführt ist:
https://de.wikipedia.org/wiki/Fuzzy_C-Means

Praktische Implementierung

Die Umwandlung eines solchen Algorithmus in ausführbaren Code stellt natürlich eine größere Herausforderung da. Dazu müssen alle Variablen vorhanden und sinnvoll initialisiert sein, am besten an Abhängigkeiten gekoppelt. Der Algorithmus an sich wird anschließend Schritt für Schritt implementiert.

Relevante Variablen:

numDataPoints(int):
Die Anzahl der Merkmalsvektoren, im Beispiel der Bildanalyse ist das die Anzahl der Pixel.
numClusters(int):
Die Anzahl der Cluster. Diese wird entweder vorgegeben oder durchiteriert.
numDimensions(int):
Die Dimensionalität der Merkmalsvektoren. Im Beispiel der Bildanalyse sind es die Werte für rot, grün und blau, also ist die Anzahl der Dimensionen 3.
degreeOfMembership(double[numDataPoints][numClusters]):
Zugehörigkeitsmatrix. Speichert für jeden Datenpunkt die Anziehungskraft der einzelnen Cluster.
epsilon(double):
Genauigkeitsparameter. Umso höher die geforderte Genauigkeit, desto mehr Iterationen muss der Algorithmus durchlaufen.
fuzziness(double):
Toleranz beim Clustern. Erlaubt, dass Cluster "weiche" Grenzen besitzen, also Merkmalsvektoren mehreren Clustern zu einem gewissen Teil zugehörig sein können.
dataPoints(double[numDataPoints][numDimensions]):
Die Merkmalsvektoren.
clusterCenter(double[numClusters][numDimensions]):
Die Positionen der Clusterzentren. Im Beispiel der RGB-Analyse enthalten sie den Farbwert (die Position).

Im Programm werden zuerst alle Parameter initialisiert.
Dazu gehört die Zufallsinitialisierung der Zugehörigkeitsmatrix. Dabei wird jedem Datenpunkt für jede Dimension ein Zufallswert zwischen 0 und 1 zugewiesen, die Summe über alle Dimensionen beträgt dabei 1. Durch die Zufallsinitialisierung müssen sich im ersten Iterationsschritt die Gewichte verändern, da die Cluster keinerlei Zusammenhang besitzen.
Außerdem werden alle anderen oben genannten Variablen initialisiert.

Ab hier übernimmt ein Loop, der solange läuft, bis die Abbruchbedingung "Epsilon ist größer als die letzte mittlere Änderung aller Zugehörigkeiten" erfüllt ist.
Er potenziert die aktuellen Zugehörigkeitswerte mit der Fuzzyness und berechnet anhand dieser neuen Gewichtungen die neuen Werte für die Clusterzentren.
Dann aktualisiert er die Gewichtungsmatrix anhand der neuen Clusterzentren und berechnet den mittleren Fehler.

Visualisierung

Die Visualisierung der Clusteranalyse wurde so implementiert, dass man Schritt für Schritt durch die Optimierungsschritte iterieren kann. So erkennt man sehr gut, wie die Zugehörigkeitsmatrix zu Beginn komplett zufällige Werte enthält und sich nachfolgend die Clusterzentren bilden und bewegen.
Nachfolgend sind Screenshots des Programms von sieben Iterationsschritten. Dabei ist der RGB-Wert der einzelnen Datenpunkten abhängig von der Clusterzugehörigkeit. Cluster 1 definiert den Rotwert, Cluster 2 den Grünwert und Cluster 3 den Blauwert.


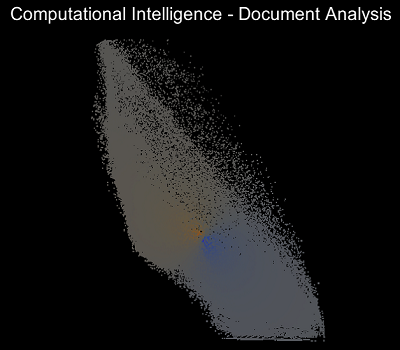
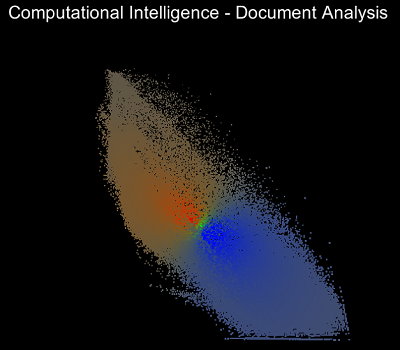
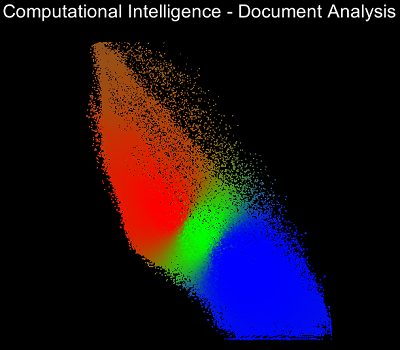
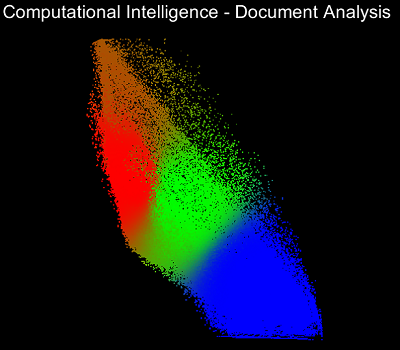
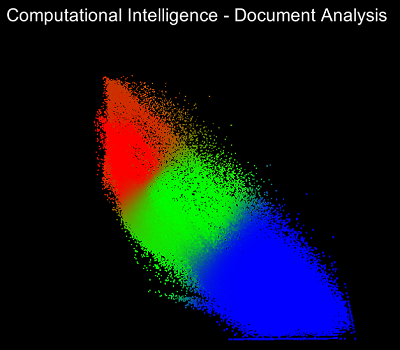
Quellen: Screenshots von eigenem Programm

Berechnung des Ergebnisses

Die Clusterzentren geben die Hauptfarben des Bilds an. Mit den Informationen des Programms kann man zusätzlich herausfinden, wieviele Merkmalsvektoren sich am meisten zu welchem Cluster zugehörig fühlen.
Anhang dieser Informationen kann man nun durch Schwellwerte Schlussfolgerungen treffen, ob ein Bild farbig, bitonal oder in Graustufen ist.

Fuzzy-k-means ist natürlich nicht optimal um diese Schlussfolgerung zu treffen. Dazu würde schon ein Histogramm über alle Farben reichen, das spart Zeit und Aufwand. Dies ist nur ein Lernbeispiel, da sich mit Bildern und dem RGB-Farbraum die Funktionsweise der Clusteranalyse besser darstellen lässt. Höherdimensionale Räume und Merkmale wie Kundendaten lassen sich schlecht visualisieren, funktionieren aber auf dieselbe weise.