Tutorium Mathematik 2
Kurven in Parameterdarstellung, Kegelschnitte - Lösungen
| 2.1 Gegeben ist folgender impliziter Funktionsausdruck: 9x^2 + 16y^2 - 32y - 128 = 0 a) Zeigen Sie, dass diese implizite Funktion eine Ellipse beschreibt, indem Sie die gegebene Gleichung in die Normalform einer Ellipsengleichung bringen ! b) Geben Sie die Koordinaten des Zentrums der Ellipse und der Brennpunkte an! c) Fertigen Sie eine Skizze an ! d) Zeigen Sie, dass der Punkt P (12/5; 17/5) auf der Ellipse liegt ! e) Berechnen Sie den Anstieg, den die Funktionskurve in diesem Punkt P hat. Differenzieren Sie dazu den impliziten Funktionsausdruck ! Lösung: a) 9x^2 + 16y^2 - 32y - 128 = 0 quadratische Ergänzung: 9x^2 + 16(y-1)-16-128=0 9x^2 + 16(y-1)^2-144=0 x^2/16+((y-1)^2)/9=1 b) Zentrum: Z(0;1) Brennpunkte: e^2=16-9=7 e=+-√7=+-2,65 F1(2,65;1) F2(-2,65;1) c) 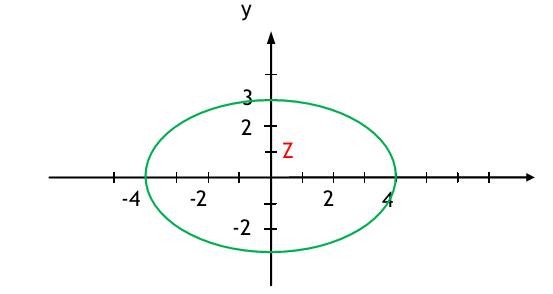 2.2 Gegeben ist eine Ellipse mit dem Zentrum Z(3;2) und den Halbachsen α = 6 (parallel zur x-Achse) und b = 3(parallel zur y-Achse). a) Geben Sie die Ellipsengleichung in impliziter Form und Parameterform an. b) Skizzieren Sie die Ellipse und berechnen Sie die Brennpunkte. c) Finden Sie die Schnittpunkte der Ellipse mit der y-Achse und geben Sie dort die Gleichungen der Tangenten an die Ellipse an. Lösung: a) implizite Form: (x-3)^2/36 + (y-2)^2/9 = 1 Parameterform: x=6*cost+3 y=3*sint+2 t ist Element von 0;2pi b) 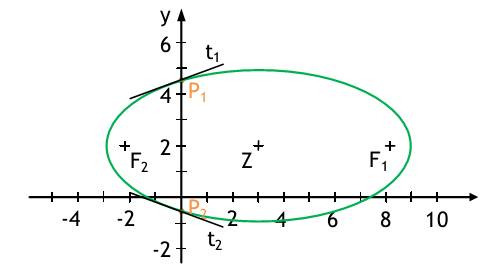 e^2=a^2-b^2=36-9 e^2=27 e=+-√27=+-5,2 Brennpunkte: F1(8,2;2) F2(-2,2;2) c) Schnittpunkte der Ellipse mit der y-Achse: x=0-> (0-3)^2/36 + (y-2)^2/9 = 1 9/36 + (y-2)^2/9 = 1 I :36 9+4(y-2)^2=36 I-9 4(y-2)^2=27 I:4 (y-2)^2=27/4 (y-2)=+-3/2√3 y1=2+3/2√3=rund 4,6 -> P1=(0:4,6) y2=2-3/2√3=rund -0,6 -> P2=(0;-0,6) Gleichungen der Tangenten: Ellipsengleichung differenzieren: 2/36(x-3)+2/9(y-2)y'=0 y'=36/(2/9(y-2))=9/36*((x-3)/(y-2))=1/4*((x-3)/(y-2)) P1: y'(P1)=-1/4*((-3)/2,6)=rund 0,29 t1: y1=0,29x+4,6 P2: y'(P2)=-1/4*((-3)/2,6)=rund 0,29 t2: y2=-0,29x-0,6 2.3. Gegeben ist folgende Kurve 2. Ordnung:9x^2-18x+9y^2-72=0 a) Bringen Sie diese Gleichung in eine geeignete Form um zu beurteilen, um welche Art Kegelschnitt es sich handelt. b) Schreiben Sie die Gleichung des Kegelschnittes in Parameterform. c) Berechnen Sie den Anstieg der Kurve an x=0 (Differenzieren der impliziten Funktionsgleichung) und geben Sie dort die Tangentengleichung(en) an. d) Fertigen Sie eine Skizze an Lösung: 9x^2-18x+9y^2-72=0 9(x-1)^2-9+9y^2-72=0 9(x-1)^2+9y^2=81 (x-1)^2+y^2=3^2 -> Kreis mit dem Mittelpunkt M(1,0) und Radius R=3 x=1+3cos(t) y=3sin(t) t ist Element von 0; 2pi 9x^2-18x+9y^2-72 = 0 I d/dx 18x-18+18yy' = 0 y' = (1-x)/y Schnittpunkt mit y-Achse x=0 -> 9y^2=72 y=+-2√2 y'(0)=1/y=1/+-2√2=+-1/4√2 Tangente an S1 (0;2√2) y=1/4√2x+2√2 Tangente an S2 (0;-2√2) y=-1/4√2x-2√2 2.4 Eine Hyperbel soll symmetrisch zu den Koordinatenachsen verlaufen und ein Scheitelpunkt soll S(4/0) sein. Außerdem sei y=2x eine Asymptote. Geben Sie die Gleichung der Hyperbel in der impliziten Normalform und in der Parameterform an. Lösung: Scheitelpunkt auf x-Achse, also ist Hyperbel nach rechts und links geöffnet mit der Form: (x^2/a^2)-(y^2/b^2)=1 a=Strecke OA = 4 Anstieg der Asymptoten: b/a = 2 -> b=8 Implizite Normalform:x^2/16-y^2/64=1 Parameterform: x=+-4cosh(t) y=8sinh(t) t ist Element von R |
| PDF Dokument Lösungen Parameterdarstellung |
Diese Seite wurde noch nicht kommentiert.





